摘  要  爐頂布料制度是高爐最重要的制度，而布料溜槽的形式對布料存在關鍵性影響，目前溜槽形式有橫截面半圓形溜槽和方形，本文通過對兩種溜槽的進行了對比，通過matlab軟件模擬計算找出了不同溜槽的布料特點，為溜槽的使用和角度選擇提供了依據。

關鍵詞  高爐  溜槽  matlab

1  概述

邯鋼煉鐵部五高爐有效容積為2000m3高爐，2005年由1260m3高爐改造而成，采用全皮帶上料，爐頂并罐式料罐。并罐布料偏析是由于爐料進入料罐后流動產生粒級偏析，布料過程中料流在溜槽上偏析布引起，主要表現在爐料在料面上的落點軌跡和圓周方向的料流流量[1]，并罐形式爐頂布料由于料罐中心線與產生較大偏析，由于并列料罐的布置，爐料從料流閥流出后下落到中心喉管，在中心喉管偏行，這樣在溜槽一圈的旋轉中，爐料落到溜槽上的速度和落點都不同，這就導致爐料在料面上的質量分布不均勻[2]，但由于布料過程中產生一定的布料偏析，特別是由于半圓形圓周摩擦力較小，導致爐料布料落點范圍較寬，休風后發現整個溜槽中部出現爐料摩擦的痕跡，說明整個布料過程爐料已經出現脫離溜槽布料控制的情況，高爐后期通過對礦批和焦批的調整后取得了一定的效果，但礦批和焦批有一定的局限性。后設計使用方溜槽，方形溜槽由于邊緣直角形，邊緣力較大，可以將爐料很好控制，落點較集中，但由于前期沒有使用過方溜槽，布料角度和礦批等都需要從新衡量，因此對兩種溜槽進行了模型計算。

2  布料溜槽模擬計算

2.1圓形溜槽布料情況

圓形布料溜槽示意圖及相關受力分析見圖1。

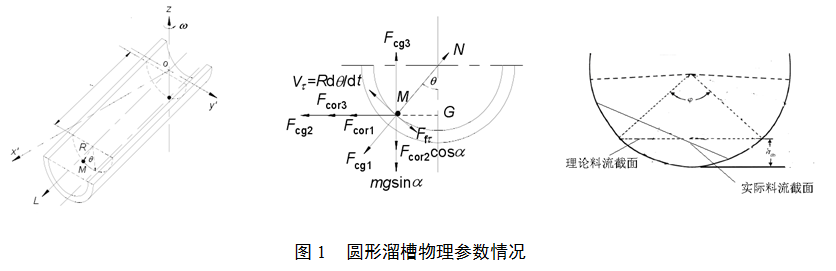
2.1.1  圓形溜槽布料數值設定

由于爐料落點主要受離開溜槽時的速度影響，因此對溜槽尾端爐料速度進行分解研究，可將爐料離開溜槽后速度分為x，y，z三個方向上的拋物自由落體運動，其中的vx，、vy、vz；設定料線為H，Q為爐料流量kg/s，S為料流開口面積m2，ρ為密度kg/m3，高爐布料溜槽轉速 圈/7.5s，中心喉管高度h為2m，a為旋轉溜槽傾角，λ為消減系數。；α(°)為旋轉溜槽傾角； L0 (m)為溜槽有效長度；ω(rad/s)為溜槽旋轉角速度；μ為溜槽對爐料的摩擦系數。高爐布料相關情況見表1。

2.1.2  圓形布料溜布礦模型計算

圓形布料溜槽布礦模型計算公式及相關參數：

Vk1= 

Vk2= （Vk1* Vk1+0.5*g*h）1/2

VK3=λ* Vk2*cosa

VK4= (2*g*(cosα-μ*sinα)*L0+4*π2*ω2*sinα*(sinα+μ*cosα) *L02+v32)1/2

Vx=Vk4*sina

Vy=Vk4*cosa

圓溜槽計算時最高點和最低點的爐料所圍成區域組成爐料布料區域，5高爐目前使用圓溜槽半徑0.97m，計算橫截面積0.3695m2，由于爐料面積0.0629 m2，如爐料堆積過程中兩端呈直角，則爐料堆積面積為0.0671 m2，與爐料橫截面積較為接近，因此本模型取爐料兩端為直角。通過角速度w和溜槽長度計算出最高點位于0.44m，最低點處于溜槽橫截面中心，本次計算忽略溜槽本身厚度影響，計算如表1，通過MATLAB模擬計算51和50度角時最遠位置布料、最近位置和料寬見表2。

2.1.3  圓形布料溜槽布焦模型計算

圓形布料溜布焦模型計算公式及相關參數：

VJ1= 

VJ2= （VJ1* Vk1+0.5*g*h）1/2

VJ3=λ* VJ2*cosa

VJ4= (2*g*(cosα-μ*sinα)*L0+4*π2*ω2*sinα*(sinα+μ*cosα) *L02+v32)1/2

Vx=VJ4*sina

Vy=VJ4*cosa

通過MATLAB模擬計算51和50度角時最遠位置布料、最近位置和料寬見表3。

2.2  方形溜槽布料情況

方形布料溜槽示意圖及相關受力分析見圖2。

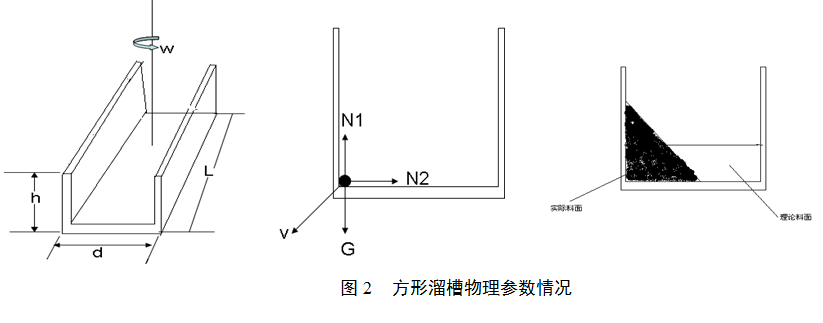
2.2.1  方形溜槽布料數值設定

設定料線為H，Q為爐料流量kg/s，S為料流開口面積m2，ρ為密度kg/m3，高爐布料溜槽轉速 圈/7.5s，中心喉管高度h為2m，a為旋轉溜槽傾角，λ為消減系數。；α(°)為旋轉溜槽傾角；L0 (m)為溜槽有效長度；ω(rad/s)為溜槽旋轉角速度；μ為溜槽對爐料的摩擦系數。

2.2.2  方形布料溜布礦模型計算

方形布料溜布焦模型計算公式及相關參數：

Vk1= 

Vk2= （Vk1* Vk1+0.5*g*h）1/2

VK3=λ* Vk2*cosa

VK4= (2*g*(cosα-μ*sinα)*L0+4*π2*ω2*sinα*(sinα+μ*cosα) *L02+v32)1/2

Vx=Vk4*sina

Vy=Vk4*cosa

方溜槽計算時最高點和最低點的爐料所圍成區域組成爐料布料區域，5高爐目前備用方溜槽長3m，內壁寬0.97m，外壁寬1.2m，高0.67m，其中下部壁厚0.14m， 計算橫截面積0.35141m2，由于爐料面積0.0629 m2，與爐料橫截面積較為接近，因此本模型取爐料兩端為直角。計算出最高點位于0.35m，最低點處于溜槽橫截面中心，通過MATLAB模擬計算51和50度角時最遠位置布料、最近位置和料寬見表4。

2.2.3  方形布料溜布焦模型計算

方形布料溜布焦模型計算公式及相關參數

VJ1= 

VJ2= （VJ1* VJ1+0.5*g*h）1/2

VJ3=λ* VJ2*cosa

VJ4= (2*g*(cosα-μ*sinα)*L0+4*π2*ω2*sinα*(sinα+μ*cosα) *L02+v32)1/2

Vx=VJ4*sina

Vy=VJ4*cosa

通過MATLAB模擬計算51和50度角時最遠位置布料、最近位置和料寬見表5。

3  不同布料溜槽模型計算結果對比

3.1布礦情模型計算結果對比

圓形溜槽布礦模型模擬軌跡如圖3，方形溜槽布礦模型模擬軌跡如圖4。

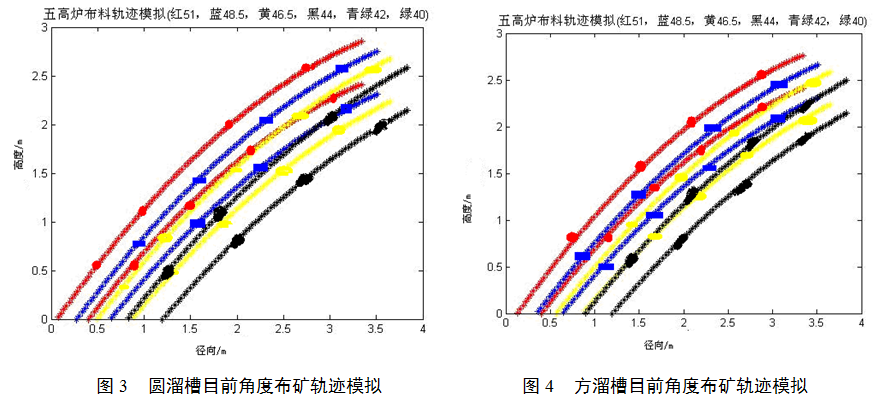
從圖3和圖4看51度角調度最外爐料落點圓形溜槽較方形溜槽靠近爐墻，布料角度相差1度圓溜槽爐料分布相差小1.2mm，隨著布料角度的縮小，兩種溜槽的布料寬度都有所增加，結果如下：

（1）圓溜槽布料角度相差1度爐料分布相差76mm，方溜槽布料角度相差1度爐料分布相差77.2mm；

（2）圓溜槽最遠點較方溜槽最遠點遠69mm；

（3）圓溜槽隨布料角度遞減過程中布料帶寬有所增加，1度角增加約11mm；

（4）方溜槽隨布料角度遞減過程中布料帶寬有所增加，1度角增加約9.8mm；

3.2  布焦情模型計算結果對比

圓形溜槽布焦模型模擬軌跡如圖5，方形溜槽布焦模型模擬軌跡如圖6；

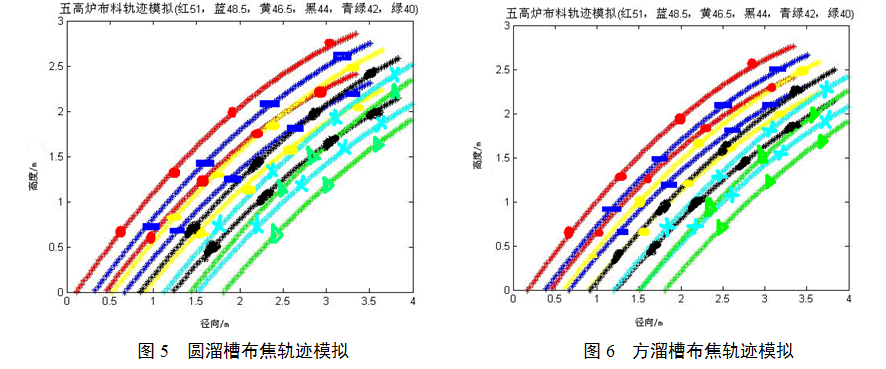
從圖5和圖6看51度角調度最外爐料落點圓形溜槽較方形溜槽靠近爐墻，布料角度相差1度圓溜槽爐料分布相差小1.8mm，隨著布料角度的縮小，兩種溜槽的布料寬度都有所增加，結果如下：

（1）圓溜槽布料角度相差1度爐料分布相差72.6mm，方溜槽布料角度相差1度爐料分布相差74.4mm，

（2）圓溜槽最遠點較方溜槽最遠點遠67mm；

（3）圓溜槽隨布料角度遞減過程中布料帶寬有所增加，1度角增加約9.4mm；

（4）方溜槽隨布料角度遞減過程中布料帶寬有所增加，1度角增加約7.6mm；

4  結語

（1）圓形溜槽布料同樣角度爐料落點較方形溜槽距爐墻更近；布焦炭圓溜槽最遠點較方溜槽最遠點遠67mm；布礦圓溜槽最遠點較方溜槽最遠點遠69mm

（2）圓形溜槽布料角度相差1度較方形溜槽布料寬度小，布焦角度相差1度相差小1.8mm，布礦角度相差1度相差小1.2mm；

（3）無論方形溜槽還是圓形溜槽，隨著布料角度遞減過程，爐料落點寬度都有所增加，圓形溜槽增加幅度更大，圓形溜槽布礦隨1度角增加約11mm、布焦增加9.4mm，方形溜槽布礦隨1度角增加約9.8mm、布焦增加7.6mm；

5  參考文獻

[1] 并罐式無鐘爐頂布料蛇形偏料的研究[J]. 杜鵬宇，程樹森，滕召杰.  北京科技大學學報. 2011(04)

[2] 無鐘并罐式高爐周向不均勻布料的研究[J]. 任廷志.  鋼鐵研究學報. 1999(03)